討論了電磁流量計矩形和鞍狀線圈所產生磁感應強度的分布情況。運用畢奧薩伐爾定律和疊加原理，通過數值仿真得到勵磁線圈在測量管道內電極橫截面上的磁場分布情況。提出磁感應強度的方向平行程度和大小均勻程度２個指標，并用其來判別感應磁場分布的均勻程度。依據以上２個指標，分別對不同尺寸的矩形和鞍狀勵磁線圈所產生的感應磁場進行計算分析和優化。

１.引 言

電磁流量計結構簡單，其內部無活動部件和阻流元件，具有可靠性高、精度高的特點，目前在冶金、石油化工、醫療、農業灌溉、城市給排水等領域都有廣泛應用。電磁流量計是利用法拉第電磁感應原理測量導電液體體積流量的儀表 ，勵磁線圈安裝在測量管道的外部，產生垂直于測量管中心軸線的感應磁場Ｂ，當導電性液體通過電磁流量計時切割磁力線，傳感器檢測電極上會產生正比于流體流速Ｖ的感應電動勢Ｅ。通常可表達為：E=KBDV,其中ｋ為儀表系數，Ｄ為測量管道內徑。

流速Ｖ之間的關系為：Ｑ＝π/4D平方V,因此Q=（πD/4KB）E0

故當磁感應強度Ｂ與管道內徑Ｄ一定時，流量Ｑ僅與流體中產生的感應電動勢Ｅ成正比，而與其它物理參數變化無關。上述公式只是簡單地說明電磁流量計的工作原理，只有滿足一定的條件時才能成立 ：（１）在無限大范圍內，磁感應強度Ｂ呈均勻分布；（２）流體速度如同固體導體一樣，其內部質點的速度處處相等，與平均流速相同。

 勵磁線圈的結構決定了電磁流量計感應磁場的分布特性，線圈和感應磁場的研究對提高電磁流量計性能具有重要意義。張小章 用理想化磁場模型對大管徑多電極電磁流量計磁場進行計算研究。

ＭｉｃｈａｌｓｋｉＡ等 利用有限元方法建立電磁流量計勵磁線圈的３Ｄ混合數學模型。金寧德等 采用有限元方法計算四電極電磁流量計磁場分布特性，并分析儀器偏心及流體磁導率變化因素對磁場分布特性影響。李斌等 給出計算矩形鞍狀線圈在測量管內磁場分布的一種折線近似算法。徐立軍等 采用有限元方法，對不同軸向長度線圈所產生激勵磁場的平行程度作分析。黃安貽等 在非均勻磁場電磁流量計基礎上，求解勵磁線圈的截面形狀，并仿真線圈的磁場。鄔惠峰等 利用有限元方法建立電磁流量計傳感器場路耦合模型，以提高勵磁系統的研究效率。滕濤等 從磁偶極子的磁場理論出發，對外流式電磁流量計和油管構成的環形空間中磁場分布情況進行數值仿真。對用于明渠測量的電磁流量計，文獻分析了鞍狀和雙甲板形狀線圈的磁場分布均勻程度以及磁場邊界效應。傅新等 介紹了一種基于測量邊界條件的分區解析式磁場重構方法，并用于電磁速度探針附近磁場的重構。

為獲得分布均勻的磁場，本文對電磁流量計矩形和鞍狀勵磁線圈的磁場分布特性進行數值分析，提出判別磁場分布均勻程度的指標，考察勵磁線圈的形狀、尺寸等因素對磁場分布特性影響，為電磁流量計勵磁線圈優化設計提供研究方法。

２.電磁流量計感應磁場計算與仿真

根據畢奧薩伐爾定律，載流導線上電流元Ｉｄｌ在點Ｐ處產生的磁感應強度ｄＢ為：

根據式（３）對電磁流量計勵磁線圈所產生感應磁場分布情況進行數值計算與仿真。以２個勵磁線圈幾何中心連線為ｘ軸，２個電極所在直線為ｙ軸，測量管中心軸線為ｚ軸，建立空間直角坐標系。在該坐標系下，計算勵磁線圈在測量管道內電極橫截面上產生的感應磁場，其步驟如下：（１）在ｘ ｙ平面上測量管道的電極橫截面內，對２個線圈之間區域進行網格化，并確定每一網格點對應的坐標值（ｘ，ｙ，０），網格劃分越細，區域內磁感應強度計算精度越高；（２）把載流導線劃分成微電流元的集合，并確定每一微電流元矢量ｄｌ的坐標（ｌ，ｌ，ｌ）；（３）計算從ｘ ｙ ｚ每個網格點到電流元的徑矢ｒ（ｒ，ｒ，ｒ）及其距離ｒ；ｘ ｙ ｚ（４）在區域內每個網格點處，分別計算第ｔ個電流元產生的磁場強度矢量在ｘ、ｙ方向上的分量Ｂｘ和

３.感應磁場均勻程度指標

由于流體運動平行于ｚ軸，磁感應強度沿ｚ軸方向的分量對電磁流量計檢測電極的感應電勢信號沒有影響，所以可忽略此分量，此時勵磁線圈在測量管道內電極橫截面上產生的磁感應強度可表示為：Ｂ＝

Ｂｘｉ＋Ｂｙｊ。因此在所考慮電極橫截面上，每點處磁感

４.矩形與鞍狀線圈感應磁場優化

４．１ 矩形線圈感應磁場的仿真及優化

對于矩形線圈，將所考慮橫截面區域劃分成４１×４１個網格，令矩形線圈的寬為 ６ｃｍ，等于管道內徑２Ｒ。每個勵磁線圈的匝數為６，厚度為２ｃｍ，２個線圈之間的距離為６ｃｍ，緊貼測量管壁，線圈中電流強度為１０ｍＡ。首先令矩形線圈軸向長度的范圍從Ｒ到８Ｒ，間隔為Ｒ；其次，在前面所確定最優尺寸４Ｒ附近，提高尺度分辨率，從 ３Ｒ到 ５Ｒ，間隔為０．２Ｒ。考查矩形線圈在測量管橫截面上的感應磁場分布情況，如表１所示。

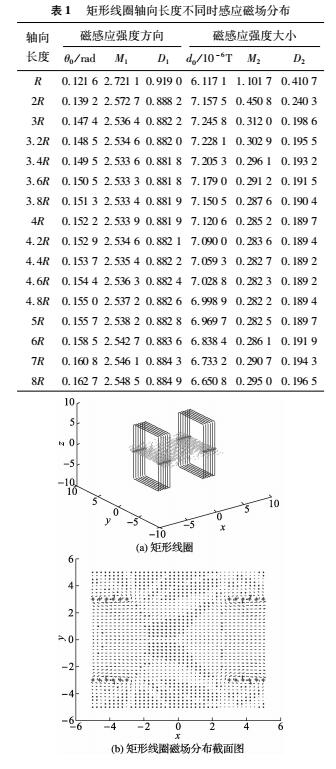
由表１可知，當矩形線圈的軸向長度為４．４Ｒ時，Ｄ２達到最小，Ｄｌ取值０．８８２２與最小值０．８８１８相差不大，表明此時磁感應強度分布更為均勻。此時矩形線圈在測量管內電極橫截面上的感應磁場分布情況如圖１所示，圖中的點為勵磁線圈與電極橫截面的交點。

４．２ 鞍狀線圈磁場的仿真及優化

對于鞍狀線圈，把電極橫截面區域劃分成４１×４１個網格，鞍狀線圈的軸向長度為 ６ｃｍ。每個勵磁線圈的匝數為６，厚度為２ｃｍ，線圈緊貼測量管壁，線圈中電流強度為１０ｍＡ。首先令線圈圓弧段的弧度范圍為９０°～１８０°，間隔１０°；其次，在前面確定最優弧度１６０°附近，提高尺度分辨率，從１５０°到１７０°，間隔２°。鞍狀線圈在電極橫截面上的感應磁場分布情況，如表２所示。

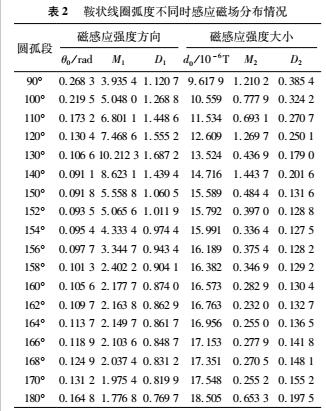
由表２可知，當鞍狀線圈圓弧段的弧度為１５４°時，Ｄ２達到最小值，Ｄ１ 取值 ０．９７４４，同時感應磁場方向指標 θ為０．０９５４，與最小值０．０９１１相差不大，綜合考慮選鞍狀線圈圓弧段的最優弧度為１５４°。

取鞍狀線圈圓弧段的弧度為１５４°，首先取線圈的軸向長度范圍Ｒ～６Ｒ，間隔為Ｒ；其次在最優尺寸２Ｒ附近，提高尺度分辨率，從 Ｒ到 ３Ｒ，間隔為０．２Ｒ。

考查鞍狀線圈在電極橫截面上的感應磁場分布情況，如表３所示。

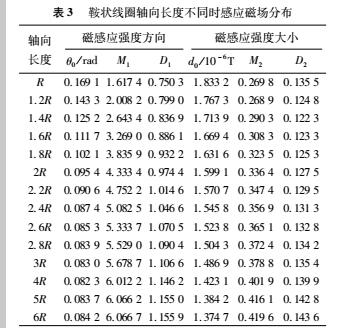
由表３可知，當鞍狀線圈的軸向長度為１．４Ｒ時，Ｄ 達到最小，Ｄ 取值０．８３６９，磁場方向指標 θ取值０．１２５２。表明鞍狀線圈軸向長度為１．４Ｒ、圓弧段的弧度為１５４°時，其感應磁場分布更為均勻。此時鞍狀線圈在測量管內電極橫截面上的磁場分布情況如圖２所示。

５.矩形與鞍狀線圈磁場對比分析

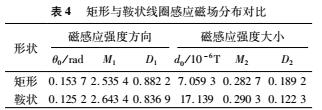
依據以上２個磁場均勻度指標，對優化后的矩形和鞍狀線圈，在電極橫截面上的磁場分布情況進行對比，如表４所示。

由表４可知，從磁感應強度方向和大小２個方面，鞍狀線圈較矩形線圈整體分布更均勻；同時鞍狀線圈可提供的感應磁場也更強。此時矩形和鞍狀線圈磁場強度方向的具體分布情況分別如圖３和圖４所示，磁感應強度大小的具體分布情況分別如圖５和圖６所示。

對比圖３和圖４，也可以略微反映出鞍狀勵磁線圈較矩形勵磁線圈磁感應強度方向整體平行程度更好，與表４中的結果一致。

對比圖５和圖６，也可看出鞍狀勵磁線圈較矩形勵磁線圈磁場強度大小整體均勻程度更好，與表４中的結果一致。

６.結 論

 為獲得分布均勻的感應磁場，在傳感器測量管道內電極橫截面上，對矩形和鞍狀線圈產生的感應磁場分布進行數值計算和仿真。提出了判別磁感應強度矢量分布均勻程度的２個指標：磁感應強度方向平行程度和大小均勻程度。依據２個表示感應磁場均勻程度的指標，對不同尺寸下的矩形和鞍狀線圈的感應磁場分布情況進行分析比較。結果表明：經過優化設計后，相比矩形線圈，鞍狀線圈產生的感應磁場分布更為均勻，同時可提供的感應磁場更強。本研究電磁流量計不同形狀、尺寸勵磁線圈產生的磁場分布特性，對勵磁線圈的優化設計具有參考意義。